By Manoj Thomas and Vicki Morwitz

t gas stations and at Wal-Mart, on television infomercials or on magazine subscription reply cards, it's common for items to be priced at $2.99 instead of $3.00, or at $99.99 instead of $100.00. Why? Can it be that economically rational consumers perceive a price ending in nine to be significantly lower than a price that is only one cent higher? This question has attracted researchers’ attention since 1932, when Louise Bader and James P. Weinland investigated the topic in the Journal of Retailing. And much research – not to mention conventional wisdom – suggests that consumers do not respond to very small price changes.

But more recent research suggests that the last digit of a price can have a significant impact on firms’ revenues. One commonly cited explanation for the popularity of nine-ending prices is that consumers underestimate their true magnitude. For example, if a product is priced at $2.99 rather than at $3.00, consumers might focus on the left digit and perceive the price to be closer to $2.00 than to $3.00. To investigate why that may be the case, we developed a conceptual framework that draws on the analog model of numerical cognition. Such a cognitive approach makes sense because it seems that the effect of a left digit change – i.e., from 3 to 2 in the above example – on magnitude perception is a consequence of the way the human mind converts numerical symbols to analog magnitudes on the mental scale.

“Because we process data from left to right, the encoded magnitude of $2.99 could, at least in some situations, be significantly less than that of $3.00.”

The analog model (also known as the holistic model) of numerical cognition suggests that when people compare two multi-digit numbers, they assess the numbers’ quantitative meaning by spontaneously mapping them onto an internal, analog magnitude scale. And this conversion affects the precision of the numbers being encoded. Our basic proposition is that the effect of price ending on magnitude perception occurs during this conversion. There are three effects that support this proposition: the left digit effect, the distance effect, and domain invariance.

The Left Digit Effect. Lets say a consumer is comparing the prices of two pens: a target pen priced at $3.00 and another pen priced at $4.00. When she automatically encodes these prices into mental magnitudes on an internal analog scale, the $3.00 price is likely to be mapped on to the lower end of this scale while $4.00 will be mapped on to the relatively higher end of the scale. But what if the target pen were priced at $2.99? Even though people read three separate digits in $2.99, these digits would be represented as one analog quantity on the internal scale. And because we process data from left to right, the encoded magnitude of $2.99 could, at least in some situations, be significantly lower than that of $3.00. One possible explanation for this left digit effect is that encoding the magnitude of a multi-digit number begins even before we finish reading all the digits, perhaps beyond consciousness. So we hypothesized (Hypothesis 1) that nine-ending prices will be perceived to be smaller than a price one cent higher only if the left-most digit changes to a lower level (e.g., $3.00 to $2.99) but not if the left-most digit remains unchanged (e.g. $3.60 to $3.59).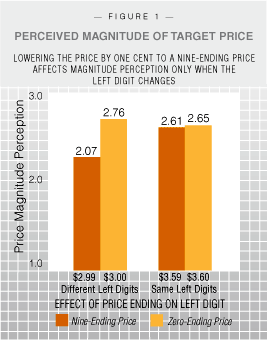

The Distance Effect. Before two numbers – the price of a target product and the price of a comparison standard product (e.g., a competing product) – can be compared, the numerical symbols must be mapped onto the internal analog scale. The closer the perceived distance between the two analog magnitudes, the greater the difficulty in discriminating between them – and the more time it takes to compare them. This phenomenon has been labeled the distance effect. A 1981 study showed that when asked to judge whether a given two digit number is higher or lower than 55, participants took significantly more time to judge numbers in the 40-70 range than in the 10-40 or 70-100 ranges. So we hypothesize (Hypothesis 2) that a left digit change caused by a nine ending price is less likely to affect the price’s magnitude perception when the comparison standard is perceived to be far apart. Stated simply, $4.00 versus $5.00 is not quite the same as $3.99 versus $5.00; but $4.00 versus $10.00 may not be perceptibly different from $3.99 versus $10.00.

Domain Invariance. Past research has often attributed the popularity of nine-ending prices to tried-and-true retailing practices. Based on a survey of published material and informal conversations with consumers and retailers, Robert Schindler of Rutgers University proposed a list of 14 meanings that price endings are likely to communicate to consumers, such as “low price,” “discount price,” or “low quality.” But if consumers’ favorable responses to nine-ending prices are solely based on such images, then these effects should be confined to the domain of prices. On the other hand, if these effects are, at least partly, due to left-to-right processing, then they should be seen in other areas. So, we hypothesize (Hypothesis 3) that decreasing the distance between the numbers being compared will increase the left digit effect not only in the domain of prices, but also in other types of nine-ending numbers.

Pricing Pens

We set out to test our hypotheses through a series of tests in which we asked students to evaluate prices. First, we asked 52 undergraduate students from a large Northeastern university to examine and evaluate prices for four pens: two ballpoint pens and two fountain pens. In each category, one brand was the target and the other was the comparison standard pen. Half the participants saw nine-ending prices ($2.99 and $3.59) and half saw zero-ending prices ($3.00 and $3.60) for the target pens. The price of the target ballpoint pen was chosen such that the price-ending manipulation resulted in a nine-ending price with a lower dollar-digit ($3.00 vs. $2.99), while that of the target fountain pen was chosen so that the nine-ending manipulation did not affect the dollar-digit ($3.60 vs. $3.59). The prices for the comparison standards were always held constant at $4.00.

Participants were given a booklet with advertisements for all four pens with price, inclusive of delivery charges. Participants then indicated the degree to which they agreed or disagreed – on a five point scale from one equaling “strongly disagree” and five equaling “strongly agree.” – with the following statement, “_____ pen’s price is high” for each brand and type of pen. We found that nine-endings increased the difference in perceived price magnitude between the zero- and the nine-ending prices only when the dollar digit changed, supporting Hypothesis 1 (See Figure 1).

Next, 63 undergraduate students from a large Northeastern university were asked to compare two brands in each of three different categories of writing instruments: fountain pens, ballpoint pens, and pencils. Target brand price level was manipulated within subjects at three different levels ($3.20 vs. $3.00 vs. $2.80); the price-ending manipulation changed the left-most dollar digit only when the price level was $3.00/$2.99. The comparison standard was $4.00 across conditions. Participants indicated their magnitude perceptions for each brand by placing an “X” on an uncalibrated 110 millimeter long horizontal line anchored at “low” and “high.” Again, the results were consistent with the left digit effect hypothesis. When the target level was $3.00, such that the nine-ending condition (i.e., $2.99) resulted in a lower dollar digit, then the nine ending price was perceived to be significantly lower. However, when the target level was $2.80 or $3.20, the nine-ending price had no effect.

Distance Effect

In a 1967 study, Stanford University psychologists Robert Moyer and Thomas Landauer measured the time participants took in comparing two Arabic numbers. They found that as the numeral distance between them decreased, the response time for the comparison task increased – a phenomenon which has come to be known as the distance effect. The distance effect should exacerbate the primacy effect of left digits. The closer the prices being compared, the higher the cognitive load, and therefore the greater the error there would be in encoding their magnitudes. We set out to test this hypothesis by asking 154 undergraduate students to evaluate two brands of pens sold by an online company. We used the same dependent measure of perceived price magnitude employed in the first study.

e manipulated the target brand’s price ending ($3.99 or $4.00) and the comparison standard’s price level ($2.00, $3.00, $5.00, or $6.00). The comparison standards were selected such that they were either $2.00 higher or lower or $1.00 higher or lower than the target price. For all levels of comparison standard, nine-ending target prices were perceived to have lower magnitude than zero-ending ones. And when the distance between the target and the comparison standard was small, i.e. $1.00, there was a significant difference in the magnitude perceptions of nine- and zero-ending prices. But there was no significant difference between these prices when the distance was $2.00. The results of this study are consistent with our assertion that the underestimation caused by the left digit effect occurs during the magnitude encoding process.

Non-Price Domains

“Retailers and advertisers have always known that there’s a great deal of psychology involved in marketing and pricing a product optimally.”

In a third study, we examined the process underlying the left digit effect and also tested whether the left digit effect manifests in non-price domains. Participants were asked to judge whether a given three digit number, between 1.00 and 9.00, was lower or higher than 5.50. We predicted that participants would take significantly more time to make magnitude judgments when the target number was closer to 5.50. More importantly, we also examined how the response times varied for nine-ending numbers.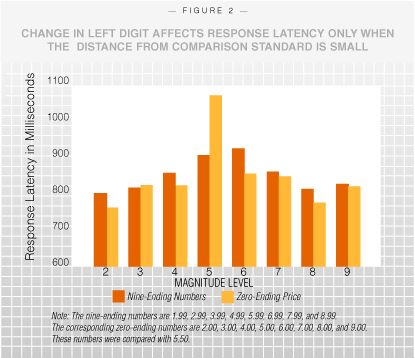

Sixteen numbers were chosen as target numbers, half with nine- and half with zero-endings, ranging from 1.99 and 2.00, to 8.99 and 9.00. Fifty-three undergraduate students from a large Northeastern university were then asked to judge whether a target number presented on a computer screen was higher or lower than the comparison standard 5.50. (The comparison standard was not presented on the screen.) The computer recorded the time participants took to click one of two buttons labeled “HIGHER” and “LOWER” as the numbers flashed on the screen. Participants took more time to make comparisons when the target numbers were close to the comparison standard. For numbers lower than 5.50, as the magnitude increased towards 5.50, the response latency (in milliseconds) also increased. (See Figure 2). For numbers higher than 5.50, the response latency systematically decreased as the magnitude increased away from 5.50. These observations suggest that the closer the number to the comparison standard, the greater the difficulty in magnitude comparisons. More interesting was the significant interaction between distance and number ending. When the magnitudes of the target numbers were four or lower, then nine-endings did not affect response times. However as we predicted, in the case of 4.99 versus 5.00, a change in left digit significantly reduced the response time, and in the case of 5.99 versus 6.00, a change in left digit significantly increased the response time.

There’s more to the story of nine-ending digits. For example, it is the psychological distance between numbers and not the nominal distance that affects how they are processed, and the psychological distance depends on the reference frame. Say a person is comparing three numbers. Whether the number five is perceived to be high or low will depend on whether the stimulus range is 0-6 or 4-10. We conducted studies in which we asked study participants to compare the quality rating of three products. And when the psychological distance between the product’s rating and the stimulus endpoints was low, the nine-ending effect was strong.

Sure it’s tempting to scoff at seemingly transparent strategies to price a gallon of gasoline $2.99 instead of $3.00, or a pair of jeans at $69.99 instead of $70.00. But retailers and advertisers have always known that there’s a great deal of psychology involved in marketing and pricing a product optimally. Some observers may continue to think that a penny doesn’t make much of a difference to consumers who are making purchasing decisions. But because of the way humans process numeric information, sometimes a penny can be worth a lot more than one cent.

Vicki Morwitz is an NYU Stern professor of marketing and the Robert Stanksy Faculty Research Fellow. Manoj Thomas is a doctoral candidate in marketing at NYU Stern.

This article is adapted from an article that appeared in the June 2005 issue of the Journal of Consumer Research.